Sometimes it becomes a challenging task to find the derivative of functions by hand. That’s where computation mathematics comes into play. There are various software available but here in this article, we try to learn how can we find derivatives using sage math.
The ‘derivative()’ and its alias ‘diff()’ is used in sage math for the computation of derivatives. In this article, we will elaborate on the first-order derivative, higher-order derivatives, derivatives at single and multiple points, partial derivatives, and derivatives of implicit functions.
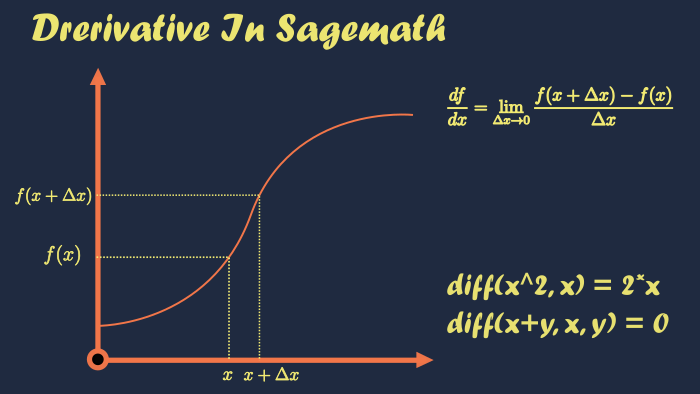
First Order Derivative of a function
In sage math, we use diff or derivative functions for finding derivatives. These are built-in functions which offer the same functionality.
To calculate the derivative of function ‘f’ w.r.t. ‘x’, we use syntax diff(f, x), where ‘f’ is the dependent variable and ‘x’ is the independent variable.
Example: Suppose we want to find the derivative of \(sin(x)\), we will use the following code:
Input:
f(x)= sin(x)
diff(f, x)
Output:
cos(x) If there are constants in the function, then we have to declare them along with other variables, and when we take the derivative of the dependent variable w.r.t. independent variable, the ‘diff()’ function considers other variables as constants.
Example: Let us find the derivative of \(y = acos(x)+bsin(x)+csec(x); a,b,c = constants\), we will utilize the following code:
Input:
x, y, a, b, c = var ('x y a b c')
y = a*cos(x)+b*sin(x)+c*sec(x)
diff(y,x)
Output:
c*sec(x)*tan(x) + b*cos(x) - a*sin(x)Higher Order Derivatives
Particular Higher Order Derivative
We can also find higher-order derivatives of functions with the syntax ‘diff(function, independent variable, order)’.
Example: Suppose we want to find 3rd order derivative of \(tan(x)\), we will use the following code:
Input:
y, x = var('y x')
f = tan(x)
diff(f,x,3)
Output:
4*(tan(x)^2 + 1)*tan(x)^2 + 2*(tan(x)^2 + 1)^2Successive Higher Order Derivatives
The above syntax only calculates the particular order derivatives, but if we need successive derivatives up to the required order then we need another syntax.
Example: Suppose we need the first four successive derivatives of \(sin(x)\), we will utilize the following code:
Input:
y, x = var('y x')
f = sin(x)
[diff(f, x, n) for n in range(1,5)]
Output:
[cos(x), -sin(x), -cos(x), sin(x)]Random Higher Order Derivatives In Single List
For example if we need 2nd, 5th, 96th, and 109th order derivative of \(sin(x)\) then following code can be utilized:
Input:
y, x = var('y x')
f = sin(x)
[diff(f, x, n) for n in [2,5,96,109]]
Output:
[-sin(x), cos(x), sin(x), cos(x)]Derivatives at Points
Derivative at a single point
Sometimes we need a derivative of a function at a particular point, this can be achieved in sage math in different ways, and here we discuss two of them.
First, we take the derivative of the function, then we use diff(f).subs(x=point) or diff(f(x=point)).
Example: Suppose we want to find the derivative of \(x^2\) at \(x=0\), we will use the following code:
Input:
x = var('x')
f(x) = x^2
diff(f).subs(x=0)
Output: 0
OR
Input:
x = var('x')
f(x) = x^2
diff(f(x=0))
Output: 0Derivative at multiple Points
We can also find the derivative of functions at multiple points using the list of Python. For example, we can differentiate \(sin(x)\) at points \([0, \frac{\pi}{2}, \pi, \frac{2\pi}{4}, 2\pi]\) with following code:
Input:
x, y = var('x y');
f = diff(sin(x),x)
[f(x=i) for i in [0,pi/2,pi, 2*pi/4, 2*pi]]
Output:
cos(x)
[1, 0, -1, 0, 1]Partial Derivative
We can find the partial derivatives of functions with the same command ‘diff’ in sage math, If we have a function \(f(x, y)\), then ‘diff(f, x)’ will give a partial derivative of \(f\) w.r.t. \(x\), and ‘diff(f,y)’ will give partial derivative of \(f\) w.r.t. \(y\).
First Order Partial Derivatives
Example: Suppose we need derivative of \(f(x,y)=yx^2+y^2x\) w.r.t \(x\), we will apply following code:
Input:
y, x = var('y x')
f = y*x^2+y^2*x
diff(f,x)
Output:
2*x*y + y^2
Example: The partial derivative of \(f(x,y)=yx^2+y^2x\) w.r.t. \(y\) can also be found by using the following code:
Input:
y, x = var('y x')
f = y*x^2+y^2*x
diff(f,y)
Output:
x^2 + 2*x*y
Higher Order Partial Derivatives
Higher order partial derivative can also be determined with the command ‘diff(f, x, order)’.
Example: Suppose we need third order derivative of \(f(x,y)=yx^5+y^2x^4\) w.r.t. \(x\), we will apply following code:
Input:
y, x = var('y x')
f = y*x^5+y^2*x^4
diff(f,x,3)
Output:
60*x^2*y + 24*x*y^2
A partial derivative with respect to the first variable and then with respect to a second variable can be found with the command ‘diff(f, x, y)’.
Example: Suppose we need derivative of \(f(x,y)=yx^5+y^2x^4\) w.r.t \(x\) and then w.r.t. \(y\), we will use following code:
Input:
y, x = var('y x')
f = y*x^5+y^2*x^4
diff(f,x,y)
Output:
5*x^4 + 8*x^3*y
If we have a function ‘f(x,y)’ in which we need a partial derivative of ‘x’ of order ‘2’ first, and then derivative w.r.t to ‘y’ of order ‘2’. We can use ‘diff(f, x,x,y,y)’ or ‘diff(f, x,2,y,2)’.
Example: Suppose we need second order derivative of \(f(x,y)=yx^5+y^2x^4\) w.r.t \(x\) and then w.r.t. \(y\), we will utilize following code:
Input:
y, x = var('y x')
f = y*x^5+y^2*x^4
diff(f,x,2,y,2)
Output:
24*x^2
Derivative of implicit functions
So far we discussed functions which are explicitly defined in terms of dependent and independent variables. We can also find the derivative of implicit functions with two methods.
Example: Suppose we want to find the \(\frac{dy}{dx}\) of \(xy^2-2xy+x=1\), this can be achieved in the following two ways:
First Method
Input:
y = function('y')(x);
f = x*y^2-2*x*y+x==1;
a=diff(f,x);
solve(a,diff(y,x))
Output:
[diff(y(x), x) == -1/2*(y(x) - 1)/x]Second Method
In the second method, we will use the partial derivative, as we know that \(\frac{dy}{dx} = -\frac{fx}{fy}\).
Input:
def ImplicitD(f):
fx = diff(f, x);
fy = diff(f, y);
return -fx/fy
x, y = var('x y');
f = x*y^2-2*x*y+x-1;
ImplicitD(f)
Output:
-1/2*(y^2 - 2*y + 1)/(x*y - x)
Both methods give different answers because the first method gives us a simplified answer while the second method did not. We can get a similar answer by adding the ‘full_simplify()’ command to the second method.
Input:
def ImplicitD(f):
fx = diff(f, x);
fy = diff(f, y);
return -fx/fy
x, y = var('x y');
f = x*y^2-2*x*y+x-1;
ImplicitD(f).full_simplify()
Output:
-1/2*(y - 1)/xUndefined Functions
Some functions are undefined at particular points such as the derivative of Abs(x) does not exist at point 0. We break Abs(x) into piecewise functions in different domains, and then we can find its derivative easily with the following code:
Input:
m = piecewise([((0, +infinity),x),((-infinity,0),-x)], var=x);
diff(m,x)
Output:
piecewise(x|-->1 on (0, +oo), x|-->-1 on (-oo, 0); x)
Rules For Differentiation in Sage Math
Sage math evaluate derivative by applying the following rules for differentiation:
Power Rule: diff(x^2) = 2*x
Sum Rule: diff(f+g) = diff(f)+diff(g)
Difference Rule: diff(f-g) = diff(f) – diff(g)
Product Rule: diff(fg) = f*diff(g)+diff(f)*g
Quotient Rule: diff(f/g) = g*diff(f)-f*diff(g)/g^2
Drill
You can try the given below exercises and get mastery in finding the derivatives using sage math.
1. \(y = x^2+x+1;\) find \(\frac{dy}{dx}\)
2. \(y = tan(sin (x));\) find \(\frac{dy}{dx}\)
3. \(y = cos(x)+sin(x));\) find \(\frac{dy}{dx}\) at \(x=\frac{\pi}{2}\)
4. \(y = 1+cos(x);\) evaluate \(\frac{dy}{dx}\) at points \([0, \frac{\pi}{4}, \frac{\pi}{2}, \pi, \frac{3\pi}{2}, 2\pi]\)
5. \(y = ln(x^2+1);\) find 11th order derivative and also make list of first four derivative.
6. \(x^y = e^{x-y};\) find \(\frac{dy}{dx}\)
7. \(\sqrt{x}+\sqrt{y}=\sqrt{a};\) find \(\frac{dy}{dx}\)
8. \(y^2+x^2y+ax^4 = 0;\) find \(\frac{dy}{dx}\)
9. \(x^3+x^2+xy^2+sin(y)=0;\) find \(\frac{dy}{dx}\) using partial derivatives.

1 thought on “A Comprehensive Guide to Sagemath Derivatives”