Question 2: Which of the following diagrams represent functions and of which type?
Solution:
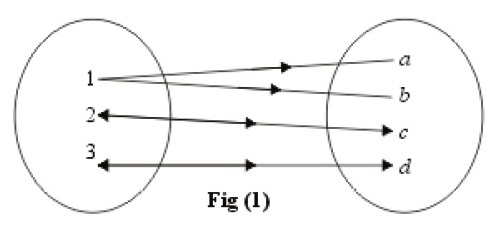
Fig (i) does not represent a function.
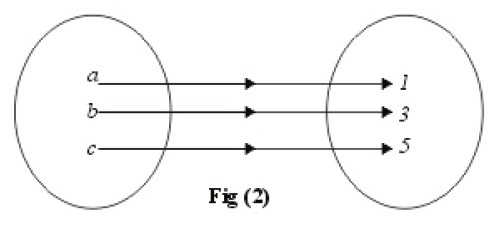
Fig (ii) is a function which bijective function.
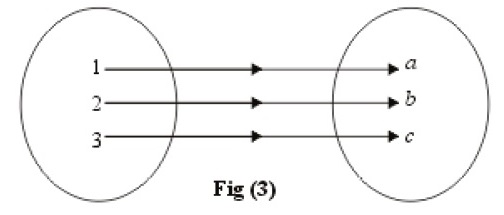
Fig (iii) is a function which bijective function.
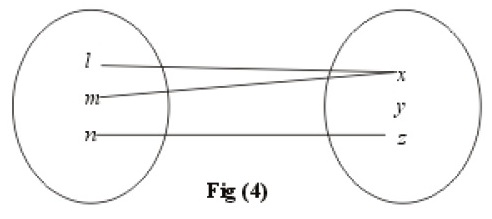
Fig (iv) is a function which is an into function.
Explanation:
Figure (i):

A function assigns exactly one output to each input.
Issue in the Figure: The input \(1\) is mapped to both \(a\) and \(b\), which violates the definition of a function, as a function must assign exactly one output to each input.
If any input goes to more than one output, it’s not a function.
Figure (ii) and Figure (iii):


Why it’s a bijection:
Each input maps to a unique output (no duplicates in outputs).
Every output has a preimage (no output is left unmapped)
Count inputs and outputs — if they are equal and each element matches perfectly, it’s bijective.
Figure (iv):

A function is into if not all outputs are used.
What the figure shows: One element \(y\) in the codomain has no preimage (i.e. no input maps to it).
Check the codomain — if some outputs are not used, it’s an into function.
