Question # 01: For \(A=\{1,2,3,4\}\), find the following relations in \(A\). State the domain and range of each relation.
\((iv)\) \(\;\) \(\{ (x,y)\mid x+y>5\} \)
Solution:
\(A \times A = \{(1, 1),\)\( (1, 2),\)\( (1, 3), \)\((1, 4),\)\( (2, 1), \)\((2, 2), \)\((2, 3), \)\((2, 4), \)\((3, 1), \)\((3, 2), (3, 3), \)\((3, 4), \)\((4, 1), \)\((4, 2), \)\((4, 3), \)\((4, 4) \}\)
\(R=\{ (x,y)\mid x+y>5\}\)
\(R=\{ (2,4),(3,3),(3,4),(4,2),(4,3),(4,4)\}\)
\(Dom(R)=\{2,3,4\}\)
\(Range(R)=\{2,3,4\}\)
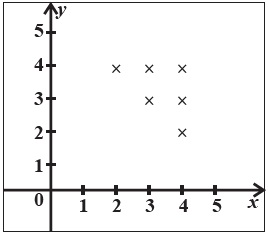
Explanation:
Start by finding the Cartesian product of set \(A=\{1,2,3,4\}\). The Cartesian product \(A\times A\) means pairing every element of \(A\) with every element of \(A\) in ordered pairs.
Now form the relation based on the condition \(x+y>5\). This means we select only those ordered pairs from the Cartesian product where the sum of the first and second elements is greater than 5, such as \((2,4),(3,3),(3,4),(4,2)\), etc.
The domain of the relation is the set of first elements in the selected ordered pairs — with no repetition.
The range of the relation is the set of second elements in the selected ordered pairs — again, with no repetition.
Note: In ordered pairs, the order of elements matters. So, \((2,4)\) is not the same as \((4,2)\), even though both have the same numbers. Their positions (first and second elements) are different.
