Note: This is the Solution of review exercise 9 from newly published book by PCTB (Punjab Curriculum and Textbook Board, Pakistan) for new 9th session 2025 Onward.
Review Exercise 9
Question # 01: Four option are given against each statement. Encircle the correct option.
\((i)\) If two polygons are similar, then:
\( a) \quad \) their corresponding angles are equal
\( b) \quad \) their areas are equal
\(c) \quad \) their volumes are equal
\( d) \quad \) their corresponding sides are equal
\( \text{Answer/Explanation}\)
\((ii)\) The ratio of the areas of two similar polygons is:
\( a) \quad \) equal to the ratio of their perimeters
\( b) \quad \) equal to the square of the ratio of their corresponding sides.
\(c) \quad \) equal to the cube of the ratio of their corresponding sides
\( d) \quad \) equal to the sum of their corresponding sides.
\( \text{Answer/Explanation}\)
\((iii)\) If the volume of two similar solids is \(125\ cm^3\) and \(27\ cm^3\), the ratio of their corresponding height is__________
\( a) \quad \) \(3:5\)
\( b) \quad \) \(5:3\)
\(c) \quad \) \(25:9\)
\( d) \quad \) \(9:25\)
\( \text{Answer/Explanation}\)
\((iv)\)\(\quad\)The exterior angle of regular pentagon is:
\( a) \quad \) \(40^\circ\)
\( b) \quad \) \(45^\circ\)
\(c) \quad \) \(60^\circ\)
\( d) \quad \) \(72^\circ\)
\( \text{Answer/Explanation}\)
\((v)\) \(\quad\)A parallelogram has an area of \(64\ cm^2\) and a similar parallegram has an area of \(144\ cm^2\). if a side of the smaller parallelgram is \(8\ cm\), the corresponding side of the larger parallegram is:
\( a) \quad \) \(10\ cm\)
\( b) \quad \) \(12\ cm\)
\(c) \quad \) \(18\ cm\)
\( d) \quad \) \(16\ cm\)
\( \text{Answer/Explanation}\)
\((vi)\) \(\quad\) The total number of diagonal in a polygon with \(9\) sides is:
\( a) \quad \) \(18\)
\( b) \quad \) \(21\)
\(c) \quad \) \(25\)
\( d) \quad \) \(27\)
\( \text{Answer/Explanation}\)
\((vii)\)\(\quad\)Two spheres are similar, and their radii are in the ratio \(4:5\). If the surface area of the larger sphere is \(500\pi\ cm^2\), what is the surface area of the smaller sphere?
\( a) \quad \) \(256\pi\ cm^2)\)
\( b) \quad \) \(320\pi\ cm^2\)
\(c) \quad \) \(400\pi\ cm^2\)
\( d) \quad \) \(405\pi\ cm^2\)
\( \text{Answer/Explanation}\)
\((viii)\)\(\quad\)A regular polygon has an exterior angle of \(30^\circ\). How many diagonals does the Polygon have?
\( a) \quad \) \( 54\)
\( b) \quad \) \( 90\)
\(c) \quad \) \( 72\)
\( d) \quad \) \( 108\)
\( \text{Answer/Explanation}\)
\((ix)\)\(\quad\)In a regular hexagon, the ratio of the length of a diagonal to the side length is:
\( a) \quad \) \(\sqrt{3}:1\)
\( b) \quad \) \(2:1\)
\(c) \quad \) \(3:2\)
\( d) \quad \) \(2:3\)
\( \text{Answer/Explanation}\)
\((x)\) \(\quad\)A regular polygon has an interior angle of \(165^\circ\). How many sides does it have?
\( a) \quad \) \(15\)
\( b) \quad \) \(16\)
\(c) \quad \) \(20\)
\( d) \quad \) \(24\)
\( \text{Answer/Explanation}\)
Question 2: If the sum of the interior angles of a polygon is \(\small{1080^\circ}\), how many sides the polygon has?
Question 3: Two similar bottles are such that one is twice as high as other. what is the ratio of their surface areas and their capacities?
Question 4: Each dimension of a model car is \(\frac{1}{10}\) of the corresponding car dimension. Find the ratio of:
\( a) \quad \) the areas of their windscreens
\( b) \quad \) the capacities of their boots
\(c) \quad \) the widths of the cars
\( d) \quad \) the number of wheels they have
Question 5: Three similar jugs have heihgts \(\small{8\ cm}\), \(\small{12\ cm}\) and \(\small{16\ cm}\). If the smallest jug holds \(\frac{1}{2}\) liter, find the capacities of the other two.
Question 6: Three similar drinking glasses have heights \(\small{7.5\ cm}\), \(\small{9\ cm}\) and \(\small{10.5\ cm}\). If the tallest glass holds \(\small{343}\) milliliters, find the capacities of the other two.
Question 7: A toy manfacturer produces model cars which are similar in every way to the actual cars. If the ratio of the door area of the model to the door area of the car is \(\small{1\ cm}\) to \(\small{2500\ cm}\), find:
\( (a) \; \) the ratio of their lengths
\( (b) \; \) the ratio of the capacities of their petrol tanks
\( (c) \; \) the width of the mode, if the actual car is \(150\ cm \) wide.
\( (d) \; \) the area of the rear window of the actual car if the area of the rear window of the model is \(3\ cm^2\).
Question 8: The ratio of the areas of two similar labels on two similar jars of cofee is \(\small{144:169}\). Find the ratio of:
\( a) \; \) the heights of the two jars
\( b) \; \) their capacities
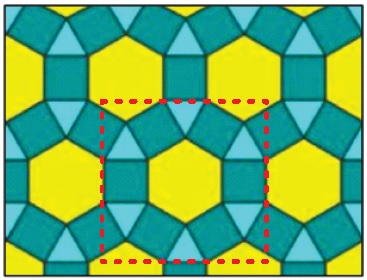
Question 9: A tesselllation of tiles on a floor has been made using a repeating pattern of a regular hexagon, six squares and six equilateral triangles. Find the total area of a single pattern with side length \(\frac{1}{2}\) meter of each polygon.