Class 9th math 9.1 solution english PCTB

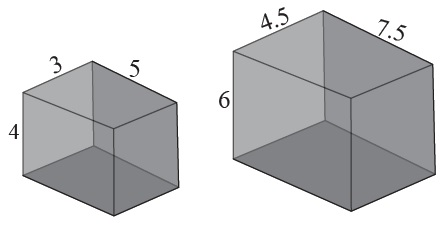
Question # 01: Find whether the solids are similar. All lengths are in cm.

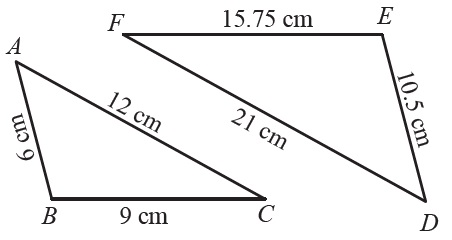
Question 2: In triangle \(\small{ABC}\), the sides are given as \(\small{m\overline{AB}=6\ cm}\), \(\small{m\overline{BC}=9\ cm}\) and \(\small{m\overline{CA}=12\ cm}\). In triangle \(\small{DEF}\), the sides are given as \(\small{m\overline{DE}}=10.5\ cm\), \(\small{m\overline{EF}=15.75\ cm}\), and \(\small{m\overline{FD}=21\ cm}\). Prove that the triangles are similar.

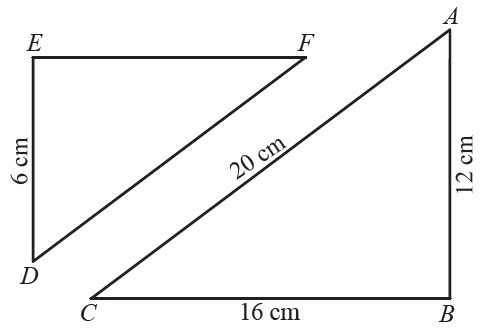
Question 3: In the figure below, \(\small{\triangle ABC\sim \triangle DEF}\). The length of \(\small{AB}\) is \(\small{12\ cm}\), \(\small{AC}\) is \(\small{16\ cm}\), and \(\small{BC}\) is \(\small{20\ cm}\). The perimeter of \(\small{\triangle DEF}\) is \(\small{30\ cm}\) and \(\small{DE}\) is \(\small{6\ cm}\). Find the length of \(\small{DF}\) and \(\small{EF}\).

Question 4: Find the value of \(\small{x}\) in each of the following:

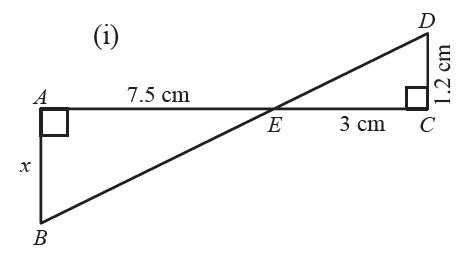
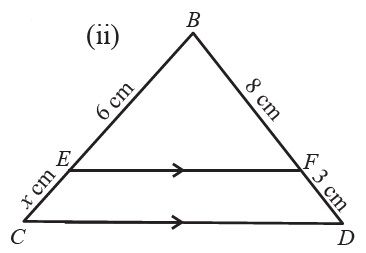
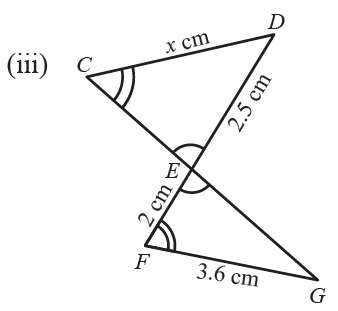
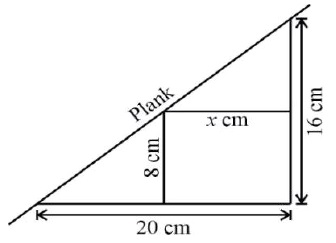
Question 5: A plank is placed straight upstairs that \(\small{20\ cm}\) wide and \(\small{16\ cm}\) deep. A rectangular box of height \(\small{8\ cm}\) and width \(\small{x\ cm}\) is placed on a stair under the plank. Find the value of \(\small{x}\).

Question 6: A man who is \(\small{1.8\ m}\) tall casts a shadow of a \(\small{0.76\ m\) in length, if at the same time a telephone pole casts a \(\small{3\ m}\) shadow, find the height of the pole.

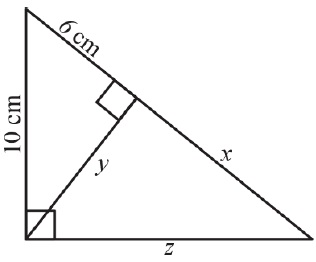
Question 7: Find the values of \(\small{x,y}\) and \(\small{z}\) in the given figure.

Question 8: Draw an isosceles trapezoid \(\small{ABCD}\) where \(\small{\overline{AB}\parallel \overline{CD}}\), and \(\small{m\overline{AB}>m\overline{CD}}\). Draw diagonals \(\small{\overline{AC}}\) and \(\small{\overline{BD}}\), intersecting at \(\small{E}\). Prove that \(\small{\triangle ABC}\) is similar to \(\small{\triangle CDE}\). If \(\small{m\overline{AB}=8\ cm}\), \(\small{m\overline{CD}=4\ cm}\), and \(\small{m\overline{AE}=3\ cm}\), find the length of \(\small{\overline{CE}}\).

Question 9: A regular dogecagon has its side lengths decreased by a factor of \(\small{\frac{1}{\sqrt{2}}}\). If the perimeter of the original dodecagon is \(\small{72\ cm}\). What is the side length of scaled dodecagon.