Question # 01: Consider the universal set \(U=\{x:x\text{ is multiple of 2 and }0<x\leq30\}\), \(A=\{x:x\text{ is a multiple of } 6\}\) and \(B=\{x:x\text{ is a multiple of 8}\}\).
\((iii)\) \(\;\) Draw a Venn diagram
Solution:
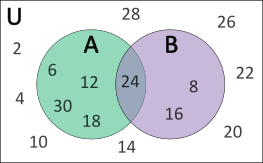
Steps to Draw a Venn Diagram
Draw two overlapping circles
- Label one circle as A (for multiples of 6).
- Label the other circle as B (for multiples of 8).
- The overlapping part shows elements common to both sets.
Find the intersection
- Find elements common to both A and B. \(A\cap B=\{24\}\)
- Write \(24\) in the overlapping region of both circles.
Fill in the unique elements of each set
- For Set A only (not in B): \(A−B=\{6,12,18,30\}\)
- For Set B only (not in A): \(B−A=\{8,16\}\)
Fill in the rest of the universal set
- These elements go outside both circles, but still inside the rectangle for \(U\): \(U−(A\cup B)=\{2,4,10,14,20,22,26,28\}\)
Enclose with a rectangle
- Label the rectangle as Universal Set \(U\).
- This contains all elements from 2 to 30 that are multiples of 2.
Student Tip:
Always start with the intersection first, then move outward.
This prevents accidental duplication and helps keep your diagram organized.
