Question 5: Let \(U=\{a,b,c,d,e,f,g,h,i,j\}\), \(A=\{a,b,c,d,g,h\}\), \(B=\{c,d,e,f,j\}\), Verify De Morgan’s Laws for these sets. Draw Venn diagram
Solution:
De Morgan’s Laws:
\( (i)\;\) \({(A\cup B)}’={A}’\cap {B}’ \)
\( (ii)\;\) \({(A\cap B)}’={A}’\cup {B}’ \)
\( (i)\;\) \({(A\cup B)}’={A}’\cap {B}’ \)
\(A\cup B=\{a,b,c,d,g,h\}\cup \{c,d,e,f,j\}\)
\(\ \ \ \ \ \ \ \ \ \ \ =\{a,b,c,d,e,f,g,h,j\}\)
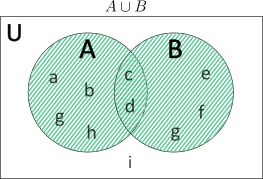
\(\text{L.H.S.}={(A\cup B)}’\)
\(\ \ \ \ \ \ \ \ \ \ \ =U-(A\cup B)\)
\(\ \ \ \ \ \ \ \ \ \ \ =\{a,b,c,d,e,f,g,h,i,j\}\)\(\ -\ \)\(\{a,b,c,d,e,f,g,h,j\}\)
\(\ \ \ \ \ \ \ \ \ \ \ =\{i\}\)

\(\text{R.H.S.}={A}’\cap {B}’\)
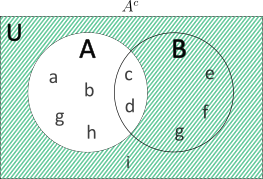
\({A}’=U-A\)
\(\ \ \ \ \ \ \ \ \ \ \ =\ \)\(\{a,b,c,d,e,f,g,h,i,j\}\)\(\ -\ \)\(\{a,b,c,d,g,h\}\)
\(\ \ \ \ \ \ \ \ \ \ \ =\ \)\(\{e,f,i,j\}\)
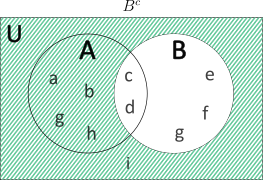
\({B}’=U-B\)
\(\ \ \ \ \ \ \ \ \ \ \ =\ \)\(\{a,b,c,d,e,f,g,h,i,j\}\)\(\ -\ \)\(\{c,d,e,f,j\}\)
\(\ \ \ \ \ \ \ \ \ \ \ =\ \)\(\{a,b,g,h,i\}\)
\(\text{R.H.S.}={A}’\cap {B}’\)
\(\ \ \ \ \ \ \ \ \ \ \ =\{e,f,i,j\}\)\(\cap\)\(\{a,b,g,h,i\}\)
\(\ \ \ \ \ \ \ \ \ \ \ =\{i\}\)
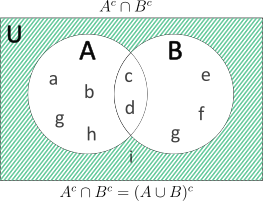
Therefore, \({(A\cup B)}’={A}’\cap {B}’ \)
\( (ii)\;\) \({(A\cap B)}’={A}’\cup {B}’ \)
\(A\cap B=\{a,b,c,d,g,h\}\cap \{c,d,e,f,j\}\)
\(\ \ \ \ \ \ \ \ \ \ \ =\{c,d\}\)
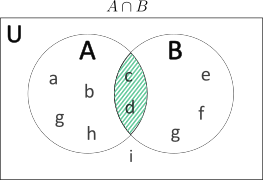
\(\text{L.H.S.}={(A\cap B)}’\)
\(\ \ \ \ \ \ \ \ \ \ \ =U-(A\cap B)\)
\(\ \ \ \ \ \ \ \ \ \ \ =\{a,b,c,d,e,f,g,h,i,j\}\)\(\ -\ \)\(\{c,d\}\)
\(\ \ \ \ \ \ \ \ \ \ \ =\{a,b,e,f,g,h,i,j\}\)
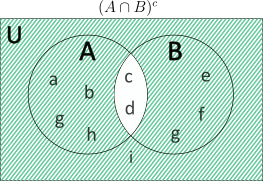
\(\text{R.H.S.}={A}’\cup {B}’\)
\({A}’=U-A\)
\(\ \ \ \ \ \ \ \ \ \ \ =\ \)\(\{a,b,c,d,e,f,g,h,i,j\}\)\(\ -\ \)\(\{a,b,c,d,g,h\}\)
\(\ \ \ \ \ \ \ \ \ \ \ =\ \)\(\{e,f,i,j\}\)

\({B}’=U-B\)
\(\ \ \ \ \ \ \ \ \ \ \ =\ \)\(\{a,b,c,d,e,f,g,h,i,j\}\)\(\ -\ \)\(\{c,d,e,f,j\}\)
\(\ \ \ \ \ \ \ \ \ \ \ =\ \)\(\{a,b,g,h,i\}\)

\(\text{R.H.S.}={A}’\cup {B}’\)
\(\ \ \ \ \ \ \ \ \ \ \ =\{e,f,i,j\}\)\(\cup\)\(\{a,b,g,h,i\}\)
\(\ \ \ \ \ \ \ \ \ \ \ =\{a,b,e,f,g,h,i,j\}\)
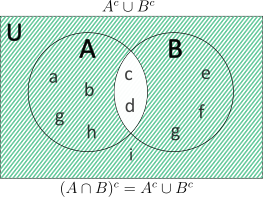
Therefore, \({(A\cap B)}’={A}’\cup {B}’ \)
